√21+ Contoh Soal Matematika Materi Bilangan Bulat Dilengkapi Kunci dan Pembahasan

Daftar Isi [Tampil]

searchsoal.com | Pada kesempatan kali ini admin akan membagikan kumpulan beberapa contoh soal matematika materi bilangan bulat dilengkapi dengan kunci jawaban dan pembahasan. Harapannya, contoh soal yang admin bagikan kali ini dapat membantu anak didik dalam mencari referensi tentang beberapa contoh soal matematika materi bilangan bulat dilengkapi dengan kunci jawaban dan pembahasan. Dan semoga contoh soal yang admin bagikan kali ini dapat memberikan dampak positif yang baik bagi perkembangan dan kemajuan belajar anak didik dalam memahami beberapa contoh soal matematika materi bilangan bulat dilengkapi dengan kunci jawaban dan pembahasan.

21+ Contoh Soal Matematika Materi Bilangan Bulat Dilengkapi Kunci dan Pembahasan

www.searchsoal.com

1. Urutan pecahan 0,8; 79%; $\frac{6}{5}$ ; 0,78 dari yang terbesar adalah ....
A. 70%; 0,78; $\frac{6}{5}$ , 0,8
B. 0,8; 79%, 0,78; $\frac{6}{5}$
C. $\frac{6}{5}$ ; 79%; 0,8; 0,78
D. $\frac{6}{5}$ ; 0,8; 79%; 0,78

Pembahasan:
Ubah setiap pecahan ke bentuk desimal:
0,8 = 0,80
79% = 0,79
$\frac{6}{5}$ = 0,83
0,78 = 0,78
Urutan pecahan dari yang terbesar adalah 0,83; 0,80; 0,79; atau $\frac{6}{5}$ ; 0,8; 79%; 0,78.

2. Bentuk sederhana dari $\frac{\frac{4}{5}-\frac{1}{3}}{\frac{1}{5}+\frac{7}{15}}$ adalah ....
A. $\frac{7}{10}$
B. $\frac{9}{10}$
C. $\frac{10}{9}$
D. $\frac{10}{7}$

Pembahasan:
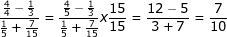
$\frac{\frac{4}{4}-\frac{1}{3}}{\frac{1}{5}+\frac{7}{15}}=\frac{\frac{4}{5}-\frac{1}{3}}{\frac{1}{5}+\frac{7}{15}}x\frac{15}{15}\\=\frac{12-5}{3+7}\\=\frac{7}{10}$

3. Pak Joko memiliki penghasilan sebesar Rp6.000.000,00 per bulan. Penghasilan tersebut digunakan untuk kebutuhan sehari-hari sebanyak $\frac{2}{3}$ bagian, untuk pendidikan anak-anaknya sebanyak $\frac{1}{4}$ dan sisanya untuk tabungan. Besar uang yang ditabung Pak Joko setiap bulan adalah ....
A. Rp2.000.000,00
B. Rp1.500.000,00
C. Rp1.000.000,00
D. Rp500.000,00

Pembahasan:
Bagian untuk ditabung
$=1-\frac{2}{3}-\frac{1}{4}\\=1-\frac{8}{12}-\frac{3}{12}\\=\frac{12}{12}-\frac{11}{12}\\\frac{1}{12}$
Besar uang yang ditabung
$=\frac{1}{12}x6.000.000\\=500.000$
Jadi, besar uang yang ditabung Pak Joko setiap bulan adalah Rp500.000,00

4. Ibu memiliki persediaan beras $5\frac{1}{6}L$ , kemudin ibu membeli lagi $1\frac{1}{3}L$ . Jika ibu dapat menggunakan 1 L beras untuk membuat 10 buah ketupat, banyak ketupat yang dapat dibuat seluruhnya adalah ....
A. 60 buah
B. 65 buah
C. 70 buah
D. 75 buah

Pembahasan:
Beras ibu:
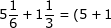$5\frac{1}{6}+1\frac{1}{3}=(5+1)+(\frac{1}{6}+\frac{1}{3})\\=6+(\frac{2}{12}+\frac{4}{12})\\=6+\frac{6}{12}=6\frac{1}{2}L\\Banyak ketupat =\frac{10buah ketupat}{1L}X6\frac{1}{2}l\\=65 buah ketupat$

5. Pak Imam memiliki sawah seluas 2.400 m². Sawah tersebut ditanami padi $\frac{5}{8}$ bagian dan ditanami kacang $\frac{1}{6}$ bagian. Jika sisa sawah ditanami tebu, luas sawah yang ditanami tebu adalah ....
A. 300 m²
B. 400 m²
C. 500 m²
D. 1.500 m²

Pembahasan:
Luas sawah = 2.400 m²
Misalkan luas sawah seluruhnya dinyatakan 1 bagian.
Bagian sawah yang ditanami tebu:
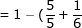$=1-(\frac{5}{5}+\frac{1}{6})\\=1-(\frac{15+4}{24})\\=\frac{24}{24}-\frac{19}{24}\\=\frac{5}{24}$
Jadi, luas sawah yang ditanami tebu adalah
$=\frac{5}{24}x2.400m^{2}\\=500m^{2}$

6. Ibu memiliki persediaan $6\frac{1}{2}$ kg terigu, kemudian ibu membeli lagi $1\frac{1}{4}$ kg terigu. Jika ibu dapat menggunakan $\frac{1}{4}$ kg terigu untuk membuat 5 buah roti, banyak roti yang dapat dibuat seluruhnya adalah ....
A. 140 buah
B. 145 buah
C. 150 buah
D. 155 buah

Pembahasan:
Terigu ibu:

$6\frac{1}{2}+1\frac{1}{4}=(6+1)+(\frac{1}{2}+\frac{1}{4})\\=7+(\frac{4+2}{8})\\=7+\frac{3}{4}=7\frac{3}{4}kg\\Banyak roti=\frac{5mbuah roti}{\frac{1}{4}kg}\\=155buah$

7. Pak Mardi memiliki sawah seluas 1.200 m². Sawah tersebut ditanami padi $\frac{5}{8}$ bagian dan ditanami kacang $\frac{1}{4}$ bagian. Jika sisa sawah ditanami tebu, luas sawah yang ditanami tebu adalah ....

A. 100 m²

B. 150 m²

C. 300 m²

D. 1.050 m²

Pembahasan:

Luas sawah = 1.200 m²

Misalkan luas sawah seluruhnya dinyatakan 1 bagian

Bagian sawah yang ditanami tebu:

$=1-(\frac{5}{8}+\frac{1}{4})\\=1-\frac{5+2}{8}\\=\frac{8}{8}-\frac{7}{8}\\=\frac{1}{8}$

Jadi, luas sawah yang ditanami tebu adalah

$=\frac{1}{8}x1.200m^{2}\\=150m^{2}$

8. Ibu memiliki persediaan $5\frac{1}{3}$ kg tepung terigu, kemudian ibu membeli lagi $4\frac{3}{4}$ kg lagi. Jika ibu dapat menggunakan $\frac{3}{4}$ kg terigu untuk membuat 9 buah roti, banyak roti yang akan dibuat seluruhnya adalah ....

A. 85 buah

B. 97 buah

C. 109 buah

D. 121 buah

Pembahasan:

Terigu milik ibu:

$5\frac{1}{3}+4\frac{3}{4}=(5+4)+(\frac{1}{3}+\frac{3}{4})\\=9+(\frac{4+9}{12})\\=9+\frac{13}{12}\\=9+1\frac{1}{12}=10\frac{1}{12}kg\\Banyak roti=\frac{9 buah roti}{\frac{3}{4}kg} x10\frac{1}{12}kg\\=121 buah$

9. Pak Rusdi memiliki sawah seluas 2.400 m². Sawah tersebut ditanami padi $\frac{4}{5}$ bagian dan ditanami kacang $\frac{1}{8}$ bagian. Jika sisa sawah ditanami tebu, luas sawah yang ditanami tebu adalah ....

A. 100 m²

B. 150 m²

C. 180 m²

D. 250 m²

Pembahasan:

Luas sawah yang ditanami tebu:

$=1-(\frac{4}{5}+\frac{1}{8})\\=1-\frac{32+5}{40}\\=\frac{40}{40}-\frac{37}{40}=\frac{3}{40}$

Jadi, luas sawah yang ditanami tebu adalah

$=\frac{3}{40}x2.400m^{2}=180m^{2}$

10. Pada tahap seleksi OSN, penilaian ditentukan sebagai berikut.

Soal dijawab benar mendapat nilai 4
Soal dijawab salah mendapat nilai -2
Soal tidak dijawab mendapat nilai -1

Dari 50 soal yang diujikan, Andi dapat menjawab 42 soal dan memperoleh nilai 118. Banyak soal yang berhasil dijawab dengan benar oleh Andi adalah ....

A. 38 soal

B. 36 soal

C. 35 soal

D. 34 soal

Pembahasan:

Misalkan jawaban benar dinyatakan dengan x dan jawaban salah dinyatakan dengan y, maka:

x + y = 42

y = 42 - x

4x - 2y - 8 = 118

4x - 2 ( 42 - x ) = 126

4x - 84 + 2x = 126

6x = 210

x = 35

11. Tanggal 1 Januari pada satu tahun kabisat jatuh pada hari Rabu. Pada tahun yang sama, Hari Kartini tanggal 21 April jatuh pada hari ....

A. Senin

B. Selasa

C. Rabu

D. Kamis

Pembahasan:

2 Januari - 31 Januari = 30 hari

1 Februari - 29 Februari = 29 hari

1 Maret - 31 Maret = 31 hari

1 April - 21 April = 21 hari

Total = 111 hari

Oleh karena 1 Minggu = 7 hari, maka 111 hari= $\frac{111}{7}=15$ minggu + 6 hari.

Jadi, misalkan tanggal 21 April ( 35 minggu + 6 hari kemudian ) adalah hari Selasa

12. Hasil dari ( -8 ) x [ 14 + ( -7 ) ] : ( 9 - 13 ) adalah ....

A. -28

B. -14

C. 14

D. 28

Pembahasan:

( -8 ) x [ 14 + ( -7 ) ] : ( 9 - 13 ) = [ ( -8 ) x 7 ] : ( -4)

= ( -56 ) : ( -4 ) = 14

13. Kota Tokyo tercatat mempunyai suhu terdingin -9⁰C dan suhu terpanas 39⁰C. Perbedaan suhu terdingin dan terpanas Kota Tokyo adalah ....

A. -48⁰C

B. -30⁰C

C. 30⁰C

D. 48⁰C

Pembahasan:

Perbedaan suhu

= suhu terpanas - suhu terdingin

= 39⁰C - ( -9⁰C )

= 48⁰C

Jadi, perbedaan suhu terdingin dan terpanas Kota Tokyo adalah 48⁰C.

14. Anisa lahir pada tanggal 3 Juni di hari Jumat. Jika Cantika lahir pada tanggal 20 September di tahun yang sama, ia lahir pada hari ....

A. Minggu

B. Senin

C. Selasa

D. Rabu

Pembahasan:

Masalah tersebut merupakan masalah yang berkaitan dengan satuan waktu. Bulan Januari, Maret, Mei, Juli, Agustus, Oktober, dan Desember terdiri atas 31 hari. Bulan April, Juni, September, dan November terdiri atas 30 hari. Bulan Februari terdiri 28 hari ( bukan tahun kabisat) dan 29 hari ( tahun kabisat ).

Jumlah hari dari 3 Juni ke 20 September:

= ( 30 - 3) hari + banyak hari pada bulan Juli + banyak hari pada bulan Agustus + 20 hari.

= 27 hari + 31 hari + 31 hari + 20 hari

= 109 hari

1 Minggu = 7 hari

Jumlah hari dari 3 Juni ke 20 September dalam minggu:

$=\frac{109}{7}$
= 15 minggu 4 hari
Oleh karena dari hari Jumat ke Jumat berikutnya merupakan 1 minggu, maka tanggal 20 September adalah 14 hari setelah hari Jumat, yaitu hari Selasa.
Jadi, Cantika lahir pada hari Selasa.

15. Pada seleksi OSN tingkat kota, peserta di berikan 50 soal pilihan ganda, dengan ketentuan penilaiannya sebagai berikut.

Soal dijawab benar mendapat skor = 4
Soal dijawab salah mendapat skor = -2
Soal tidak dijawab mendapat skor = -1

Jika Agus mengikuti seleksi tersebut dengan 4 soal tidak dijawab dan total skornya adalah 132, banyak soal yang dijawab dengan benar oleh Agus adalah ....
A. 36 soal
B. 38 soal
C. 40 soal
D. 42 soal

Pembahasan:
Tidak dijawab = 4 soal
Soal dijawab = 50 - 4
= 46 soal
Misalkan banyak jawaban benar = b soal, maka banyak jawaban salah = ( 46 - b ) soal.
Total skor = ( b x 4 ) + {(46 - b ) x ( -2)} + { 4 x (-1)}
132 = 4b + ( -92) + 2b + ( -4 )
132 = 6b + ( -96 )
132 + 96 = 6b
228 = 6b
$b=\frac{228}{6}=38$

Jadi, banyak soal yang dijawab dengan benar oleh Agus adalah 38 soal.

16. Hasil dari 26 - 24 + ( -4 ) x 2 adalah ....
A. -14
B. -6
C. 6
C. 14

Pembahasan:
26 - 24 + ( -4 ) x 2 = 26 - ( 24 : 6 ) +[( -4) x 2 ]
= 26 - 4 + ( -8 )
= 22 + (-8 ) = 14

17. Dalam kompetisi matematika, setiap jawaban benar diberi skor 2, salah -1, dan tidak dijawab 0. Diberikan soal 50 soal, Andi dapat menjawab benar 32 soal dan tidak dijawab 8 soal. Jumlah skor yang diperoleh Andi adalah ....
A. 64
B. 58
C. 54
D. 50

Pembahasan:
Jawaban benar = 32 soal; tidak dijawab = 8 soal
Jawaban salah = 50 - ( 32 + 8 )
= 50 - 40 = 10 soal
Jumlah skor = ( 32 x 2 ) + { 10 x ( -1 )} + ( 8 x 0 )
= 64 + ( -10 ) + 0 = 54

18. Hasil dari 24 - 16 : 4 + ( -3 ) x 5 adalah ....
A. -13
B. -5
C. 5
D. 13

Pembahasan:
24 - 16 : 4 + ( -3 ) x 5 = 24 - ( 16 : 4 ) + [( -3 ) x 5]
= 24 - 4 + ( -15 )
= 20 + ( -15 ) = 5

19. Dalam kompetisi OSN matematika, setiap jawaban benar diberi skor 5, salah -3, dan tidak dijawab -2. Diberikan 40 soal, Agus dapat menjawab benar soal 26 soal dan tidak dijawab 6 soal. Jumlah skor yang diperoleh Agus adalah ....
A. 106
B. 94
C. 82
D. 70

Pembahasan:
Jawaban benar : 26 soal; tidak dijawab = 6 soal
Jawaban salah = 40 - ( 26 + 6 )
= 40 - 32 = 8 soal
Jumlah skor = ( 26 x 5 ) + {6 x ( -2 )} + { 8 x ( -3 )}
= 130 + ( -12 ) + ( -24 ) = 94

20. Pada tahap seleksi OSN, penilaian ditentukan sebagai berikut.

Soal dijawab benar mendapat nilai 4
Soal dijawab salah mendapat nilai -2
Soal tidak dijawab mendapat nilai -1

Dari 50 soal yang diujikan, Andi dapat menjawab 42 soal dan memperoleh nilai 118. Banyak soal yang berhasil dijawab dengan benar oleh Andi adalah ....
A. 38 soal
B. 36 soal
C. 35 soal
D. 34 soal

Pembahasan:
Misalkan jawaban benar dinyatakan dengan x dan jawaban salah dinyatakan dengan y, maka:
x + y = 42
y = 42 - x
4x - 2y - 8 = 118
4x - 2 ( 42 - x ) = 126
4x - 84 + 2x = 126
6x = 210
x = 35

21. Tanggal 1 Januari pada satu tahun kabisat jatuh pada hari Rabu. Pada tahun yang sama, Hari Kartini tanggal 21 April jatuh pada hari ....
A. Senin
B. Selasa
C. Rabu
D. Kamis

Pembahasan:
2 Januari - 31 Januari = 30 hari
1 Februari - 29 Februari = 29 hari
1 Maret - 31 Maret = 31 hari
1 April - 21 April = 21 hari
Total = 111 hari
Oleh karena 1 Minggu = 7 hari, maka 111 hari= $\frac{111}{7}=15$ minggu + 6 hari.
Jadi, misalkan tanggal 21 April ( 35 minggu + 6 hari kemudian ) adalah hari Selasa